豁蒙楼

CS229 ICA-Implementation

发表于 更新于 分类于 Disqus：

Link: Separating mixed signals with ICA

Implementation of Independent Components Analysis

Import packages

1
2
3
4
5
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
from scipy import signal
from tqdm.notebook import tqdm

Generate the source \(S\)

\(S\in R^d\)

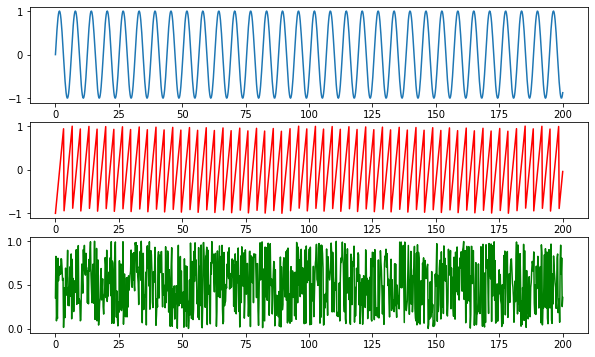
Here we choose 3 sources of signals: sine, sawtooth and noise.

1
2
3
4
5
6
7
8
9
10
11
12
13
f = plt.figure(figsize = (10,6))
ax = f.add_subplot(311)
ax2 = f.add_subplot(312)
ax3 = f.add_subplot(313)
t = np.linspace(0, 200 , 1000)
sine = np.sin(t)
sawtooth = signal.sawtooth(t*1.9)
noise = np.random.random(len(t))

ax.plot(t, sine)
ax2.plot(t, sawtooth, 'r')
ax3.plot(t, noise, 'g')
plt.show()

1
2
S = np.vstack((sine, sawtooth, noise))
S.shape
(3, 1000)

Mixture Matrix A, \(x = As\)

\(s_j^{(i)} = w_j^Tx^{(i)}\)

\(x^{(i)} = As^{(i)}\)

1
2
3
4
5
A = np.array([
  [0.5,1,0.2],
  [1,0.5,0.4],
  [0.5,0.8,1]
])
1
2
W = np.linalg.inv(A)
W
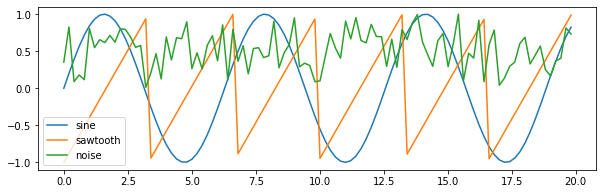
array([[-0.3       ,  1.4       , -0.5       ],
       [ 1.33333333, -0.66666667,  0.        ],
       [-0.91666667, -0.16666667,  1.25      ]])
1
X = np.dot(A.T, S)
1
2
3
4
5
6
7
plt.figure(figsize=(10,3))
plt.plot(t[:100], sine[:100])
plt.plot(t[:100], sawtooth[:100])
plt.plot(t[:100], noise[:100])
plt.legend(labels = ["sine", "sawtooth", "noise"])

plt.show()

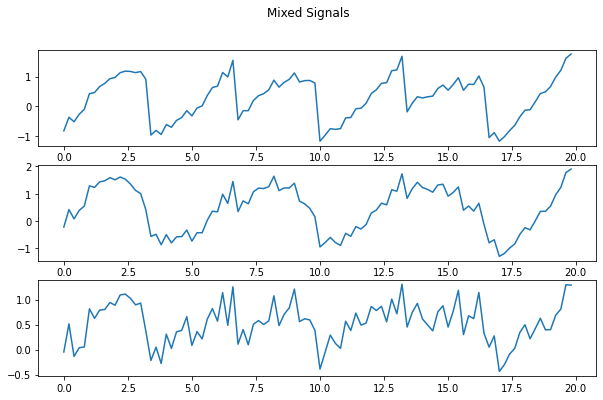
1
2
3
4
5
6
7
8
9
10
11
f = plt.figure(figsize=(10,6))
f.suptitle("Mixed Signals")
ax1 = f.add_subplot(311)
ax2 = f.add_subplot(312)
ax3 = f.add_subplot(313)

ax1.plot(t[:100], X[0][:100])
ax2.plot(t[:100], X[1][:100])
ax3.plot(t[:100], X[2][:100])

plt.show()

ICA Algorithm

1
2
3
4
5
6
7
8
9
# https://towardsdatascience.com/separating-mixed-signals-with-independent-component-analysis-38205188f2f4
def center(x):
  return x - np.mean(x, axis=1, keepdims=True), np.mean(x, axis=1, keepdims=True)

def covariance(x):
  mean = np.mean(x, axis=1, keepdims=True)
  n = np.shape(x)[1] - 1
  m = x - mean
  return m.dot(m.T) / n
1
2
3
4
5
6
7
8
# https://towardsdatascience.com/separating-mixed-signals-with-independent-component-analysis-38205188f2f4
def whiten(x):
  cov = covariance(x)
  U,S,V = np.linalg.svd(cov)
  d = np.diag(1 / np.sqrt(S))
  whiteM = np.dot(U, np.dot(d, U.T))
  Xw = np.dot(whiteM, X)
  return Xw, whiteM
1
2
def sigmoid(x):
  return 1 / (1 + np.exp(-x))
1
2
3
4
5
6
7
8
def update(W, xi, lr):
  """
  Stochastic gradient ascent, one point xi
  """
  gradient = np.dot((1 - 2 * sigmoid(np.dot(W.T, xi))), xi.T) + np.linalg.inv(W.T)
  diff = np.abs(gradient).sum()

  return W + lr*gradient, diff
1
2
3
4
5
6
7
8
9
10
def optimize(X, S, lr=0.1, thresh=1e-2, iterations=1000000):
  d, n = S.shape
  W = np.random.random(size=(d,d))
  for c in tqdm(range(iterations)):
    xi = X[:,np.random.randint(0,n-1)]
    W, diff = update(W, xi, lr)
    if (diff < thresh):
      break
  return W

1
2
3
4
5
6
Xc, meanX = center(X)
Xw, whiteM = whiten(Xc)

W_ = optimize(Xw,S)
unMixed = Xw.T.dot(W_.T)
unMixed = (unMixed.T - meanX)
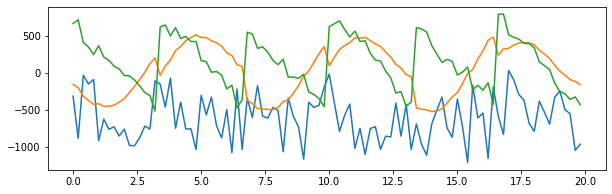
1
2
3
4
5
6
plt.figure(figsize=(10,3))
plt.plot(t[:100], unMixed[0][:100])
plt.plot(t[:100], unMixed[1][:100])
plt.plot(t[:100], unMixed[2][:100])

plt.show()

Remark

The ICA ambiguities tells us that there is no way to recover the scaling of the wi's